前言
球缺(Spherical Cap)就是在一个球上被切一刀,剩下的部分。
如下图所示,
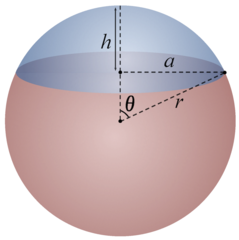 Source: Wikipedia
Source: Wikipedia
球缺就是途中浅蓝色部分。$r$是球体的半径,$a$是球缺的底面半径,$h$是球缺的高,$\theta$是球缺的极角(Polar Angle)。
| 用$r$和$h$ | 用$a$和$h$ | 用$r$和$\theta$ | |
|---|---|---|---|
| 体积 | $V={\frac {\pi h^{2}}{3}}(3r-h)$ | $V={\frac {1}{6}}\pi h(3a^{2}+h^{2})$ | $V={\frac {\pi }{3}}r^{3}(2+\cos \theta )(1-\cos \theta )^{2}$ |
| 表面积 | $A = 2 \pi r h$ | $A = \pi (a^2 + h^2)$ | $A = 2 \pi r^2 (1 - \cos \theta)$ |
单位圆盘的均匀采样
在考虑球缺表面的均匀采样之前,我们先考虑在单位圆盘均匀采样。这篇文章介绍了一种在单位圆盘均匀采样的算法。
在说明正确做法前,先来说说一个常用的错误做法。首先利用均匀采样,取得两个变量$r \in [0, 1]$和$\theta \in [-\pi, \pi]$。然后我们可以用它们表示在单位圆中的坐标为:
\[(r \cos \theta, r \sin \theta)\]我们来考虑面积的分布。对单位圆的面积公式$A = \pi r^2$求微分,可以得到:
\[dA = 2 \pi r dr\]从这个公式可以看出,$dA$和$dr$并不成线性关系,而是还有一个可变系数$r$,因此当固定角度时,在半径方向上对$r$的均匀采样并不能得到均匀的分布。因此这种采样将会获得下图的分布
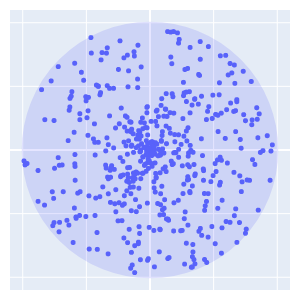
我们会发现,越靠近圆心,点越密集,这也证明了半径方向上分布不均。
如果我们把点坐标改为:
\[(\sqrt{r} \cos \theta, \sqrt{r} \sin \theta)\]那么上面的微分就变为:
\[dA = 2 \pi \sqrt{r} d \sqrt{r} = \pi dr\]$dA$和$dr$是线性关系,且$\sqrt{r} \in [0, 1], r \in [0, 1]$,所以我们得到了半径方向上的均匀分布。
而面积与角度同样是线性分布的,故最终采样的结果会像下图一样,在单位圆盘中均匀分布。
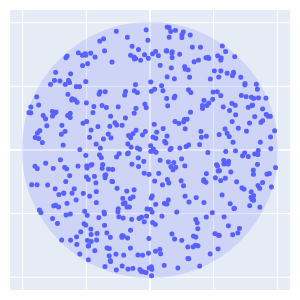
下面我们的更复杂的采样,都会基于单位圆盘的均匀采样,然后通过等面积映射,得到对应平面或曲面的均匀采样。
单位球面的均匀采样
这篇文章给出了一个等面积映射,将单位圆盘映射到单位球表面,结合上面单位圆盘的均匀采样,实现在单位球面的均匀采样。
对于单位圆盘的均匀采样得到的任意一点$(x, y)$,对应到单位球面的坐标为:
\[\left(2x \cdot r\sqrt{1-r^2 \left(x^2+y^2\right)},~2y \cdot r\sqrt{1-r^2 \left(x^2+y^2\right)},~1-2r^2 \left(x^2+y^2\right)\right)\]其中$r = 1$。
这篇文章做了一系列实验,来验证下面的几个结论:
- 从单位圆盘到单位球面的映射是等面积映射
- 单位圆盘上从圆心到圆上的射线,对应于单位球面的经度线
- 单位圆盘上的各同心圆,对应于单位球面的纬度线
- 单位圆盘的圆心$(0, 0)$,对应于单位球面的北极
- 单位圆盘上半径范围$r \in [0, \frac{1}{\sqrt{2}}]$的子圆,对应于单位球面的上半部分$(z \ge 0)$
- 单位圆盘上半径范围$r \in (\frac{1}{\sqrt{2}}, 1)$的环,对应于单位球面的下半部分$(z \lt 0)$
- 单位圆盘的圆上部分,全部对应于单位球面的南极
下面是按照上述公式采样得到的单位球面上的点。
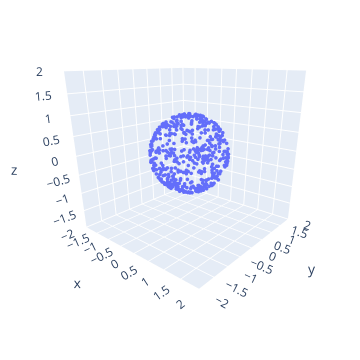
球缺的均匀采样
对于圆盘、球面、球缺,半径为r,球缺高度为h,使得他们的表面积相等,则有
\[A_d = \pi r^2 \\ A_s = 4 \pi r^2 \\ A_c = 2 \pi r h\]从上式可以看出,球面的表面积和圆盘的面积相差一个常系数,并且球缺的面积与高度成线性关系。结合第一节关于单位圆盘面积与半径方向均匀分布的讨论,假设球缺的半径为1,并且让球面表面积与球缺表面积相等,可以得到下式
\[\frac{2 \pi h}{4} = \pi r^2\]求解$r$,得到
\[r = \sqrt{\frac{h}{2}}\]代入上面球面的公式,得到
\[\left(x\sqrt{h\left(2-h\left(x^2+y^2\right)\right)},~y\sqrt{h\left(2-h\left(x^2+y^2\right)\right)},~1-h\left(x^2+y^2\right)\right)\]
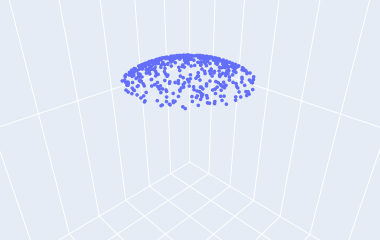
三维旋转的均匀采样
To Be Continued
参考资料
- https://en.wikipedia.org/wiki/Spherical_cap
- https://marc-b-reynolds.github.io/distribution/2016/11/28/Uniform.html
- https://marc-b-reynolds.github.io/distribution/2017/01/27/UniformRot.html
- https://mathworld.wolfram.com/DiskPointPicking.html
- https://projecteuclid.org/download/pdf_1/euclid.aoms/1177692644
- https://marc-b-reynolds.github.io/quaternions/2016/06/26/QuatNormal.html
